Stereofotos

Low Cost - Fotogrammetrie

Homepage LangLilge.de

sitemap

von Winfried Lilge, Technischer Zeichner, Shakespeareplatz 8, 27283 Verden, 52°54'44"N 9°14'10"E
Stand: 04.02.2004

1. Grundüberlegungen

Ausgehend von der erschreckenden Tatsache, dass professionelle Software zur Fotorgrammetrischen Auswertung von (Stereo-)Fotos an den Neupreis eines Kleinwagens heran reichen, mache ich mir hier Gedanken, eine billigere Lösung zu finden.

Hardware:

Ich stell mir vor, eine einfache Vorrichtung zu bauen, die eine waagerechte Verschiebung der Kamera in der Film- bzw. Bildsensor-Ebene um einen festgelegten Abstand B erlaubt. Dies sollte z.B. durch eine lineare Führung mit entsprechenden Anschlägen möglich sein, die auf ein Kamerastativ geschraubt wird. Eine Wasserwaagenlibelle zeigt die waagerechte Ausrichtung an. Dabei sind zwei Libellen oder eine Punktlibelle nötig, um Neigung und Kippung ausgleichen zu können. Eventuell ist am Stativ außerdem ein Lot befestigt, das auf den Punkt am Boden unter der linken Kameraposition zeigt, um den exakten Abstand zum Objekt messen zu können.
Die Ausrichtung der Kamera zum Stativsystem sollte möglichst stabil sein und außerdem gewährleisten, dass die Sensor-Chip-Ebene parallel zur Verschiebeachse ist.

Software:

Die Aufnahmen, die auf diesem Wege gemacht werden, sollen am Bildschirm auswertbar sein. Indem auf den zusammengehörigen Stereofotos die Bildpunkte eines Objektpunktes nacheinander angeklickt werden, werden Bildpunktpaare gebildet. Aus den Bildkoordinaten dieser Paare werden die realen Objektkoordinaten bezogen auf die linke Kameraposition durch die Software ermittelt. Es sollte eine geeignete Ausgabe der 3D-Information möglich sein, einfachsten falls als Textausgabe der 3 Koordinaten oder komfortabler gleich als VRML-Datei¹.
Die Punktwolken oder Punktverbindungen, die sich durch die Klick-Identifizierung ergeben, sollen in einer 2D-Datei gespeichert werden, um die Benutzereingaben sichern und verändern zu können. In dieser Datei sind außerdem sonstige eingetippte Informationen der Aufnahme und die Namen der Stereo-Bilder abgelegt. Im Idealfall klickt man im Explorer doppelt auf diese Datei, die Stereo-Dateien werden in die entsprechenden Bildfelder geladen und die Punkte und/oder Verbindungen zwischen Punkten werden als Vordergrundebene gezeichnet.
Um hinreichende Genauigkeit zu erzielen, werden die Koordinaten in der 2D-Datei mit einer Nachkommastelle abgelegt. Dadurch sind zehntel-Pixel-Informationen möglich.

Mögliche Anordnung in einer HTML-Datei mit JavaScript:

Linke Position: left1.jpg	Rechte Position: right1.jpg	Textausgabefeld

2. Transformationen zwischen Objektkoordinaten und Bildkoordinaten

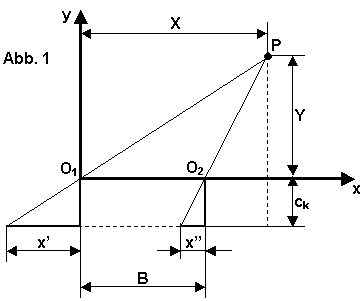
Als Abbildungsgleichungen habe ich von A. Wiedemann / TU Berlin folgende Darstellung gefunden:
Voraussetzung hierfür ist, die exakt waagerechte Verschiebung der Kamera ohne Verdrehung in irgendeiner der drei Raumachsen, weil sich sonst ungleich kompliziertere Gleichungen ergeben.
P: Objektpunkt mit (X Y Z)
O₁: linkes Projektionszentrum, Kameralinse linke Position (0 0 0)
O₂: rechtes Projektionszentrum mit (B 0 0)
c_k: Kamerakonstante, Abstand Linse - Projektionsebene
X', y': Bildkoordinaten linker Bildpunkt
X'', y'': Bildkoordinaten rechter Bildpunkt

Y B X = x' ---- = x' -------- 1.1 ck x' - x'' B Y = ck --------- 1.2 x' - x'' Y B Z = y' --- = y' --------- 1.3 ck x' - x''

         X                      X - B                   Z
x' = ck ---  1.4      x'' = ck -------  1.5     y' = ck --- = y''    1.6
         Y                        Y                     Y

y' = y''     1.7      (wegen waagerechter Verschiebung)

3. Ermittlung der Kamerakonstante c_k

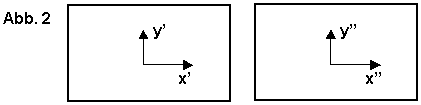Die reale Kamerakonstante bezogen auf den Abstand Objektiv-Sensorchip ist eigentlich nebensächlich, denn es kommt vielmehr darauf an, in welcher Größe die Aufnahmen später abgebildet werden. Deshalb gibt es für jeden Abbildundgsmaßstab eine eigene (Kamera-)Konstante, die folgendermaßen ermittelt werden kann:
Für alle Punkte, die sich genau 1m (bzw. eine Längeneinheit) vor der Kameralinse (Y=0) befinden, wird Y = 1. Dadurch vereinfachen sich die Gleichungen 1.4 bis 1.6 zu:

x'1m = ck X   3.1        x''1m = ck (X - B)    3.2       y'1m = ck Z = y''1m     3.3

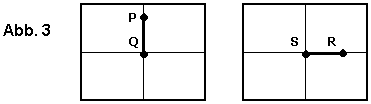	Maßstab senkrecht	Maßstab waagerecht

P = (0  1  1)   Q = (0  1  0)   |   x'P = 0    y'P = ck   |   x'Q = 0   y'P = 0
R = (1  1  0)   S = (0  1  0)   |   x'R = ck   y'R = 0    |   x'S = 0   y'S = 0

• Kamerazoom auf bestimmten Wert, z.B. Minimum oder Maximum
• Bild unbeschnitten oder reproduzierbar symetrisch beschnitten
• Ausdruck oder Bildschirmanzeige auf feste Größe eingestellt
• Bild unskaliert oder nach festgelegtem Wert (Resample)
• B nach Anschlag oder Basislineal

4. Transformationen zwischen Objektkoordinaten und VRML

VRML hat das Weltkoodinatensystem folgendermaßen festgelegt:

bzw.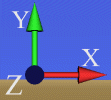

Ansicht bei Eintritt in die Szene ohne speziellen Viewpoint

bzw.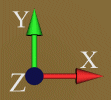

Ansicht bei Luftaufnahmen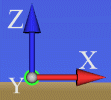

Aufnahme auf dem Boden stehend

XVRML = XArch        5.1

YVRML = ZArch        5.2

ZVRML = -YArch        bzw.        YArch = -ZVRML        5.3

5. Beispiel für bekannte Objektkoordinaten (Einheiten in m, c_k x' x'' y'' in Pixel):

P=(0,1  0,2  0,05)  =>  X=0,1  Y=0,2  Z=0,05
ck=1624
B=0,07  =>  O1=(0  0  0)  O2=(0,07  0  0)

x' =        ck X / Y =        1624 * 0,1 / 0,2 =           812
x'' =       ck (X - B) / Y =  1624 * (0,1 - 0,07) / 0,2 =  243,6
y' = y'' =  ck Z / Y =        1624 * 0,05 / 0,2 =          406

XA = x' B / (x' - x'') =  812 * 0,07 / (812 - 243,6) =   0,1
YA = ck B / (x' - x'') =  1624 * 0,07 / (812 - 243,6) =  0,2
ZA = y' B / (x' - x'') =  406 * 0,07 / (812 - 243,6) =   0,05

allercappella.de und ganainm.de sind für den Inhalt externer Links nicht verantwortlich.